密码和加密轻分享

一、密码学的发展

1. 公元前50年：凯撒密码的军事遗产

最典型的使用密码的历史故事，莫过于凯撒密码。凯撒密码是经典的替换式密码，是一种很直观的加密方式。

使用凯撒密码进行加密，只要将字母表上的每个字母向后移动特定位数找到新的字母即可。例如，

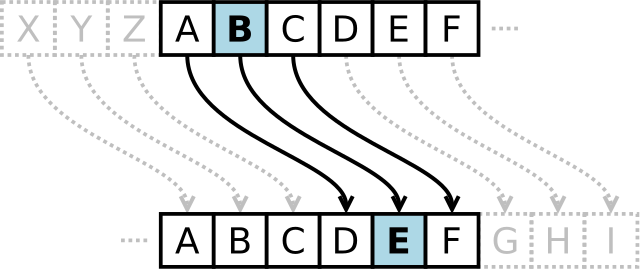
凯撒密码映射表

BYTEDANCE通过凯撒密码位移3位情况下加密结果为EBWHGDQFH。

这种思想加密还可以更复杂，比如每个字母都有特定的映射字母，如

ABCDEFGHIJKLMNOPQRSTUVWXYZ
NUVCDAGJYZTKBWFRELOSPXIHQM

这种加密方法并不是很安全，比如，26个字母在一篇文章中使用的频率是不同的，统计字频可能就能找到对应关系。

2. 1940年：图灵与恩尼格玛机的对决

我们熟知的计算机科学与人工智能之父，艾伦·图灵，在二战期间就参与了德国军事机密密码的破译工作，两年时间他的小组破译了恩尼格玛机密码系统，为盟军的军事行动提供了极大便利。

恩尼格玛机的破译是个比较长篇幅的故事，感兴趣的同学可以自行阅读。

3. 2025年：量子计算的威胁倒计时

许多经典加密算法（如RSA）是基于因数分解的，即给定一个较大的合数，分解质因数是相对困难的，而验证因数相乘结果正确性却很简单。

1000000000000000283 * 100000000000000543 = 100000000000000571300000000000153669

import time
import sys

def prime_factors(n, show_progress=False, update_interval=0.1):
    """
    分解一个正整数为其质因数的列表
    :param n: 要分解的正整数（n > 1）
    :param show_progress: 是否显示进度
    :param update_interval: 进度更新的最小时间间隔（秒）
    :return: 质因数列表
    """
    if n <= 1:
        raise ValueError("输入必须是大于1的正整数")
    
    factors = []
    num = n
    original_num = n
    last_update_time = 0  # 记录上次更新进度的时间
    
    # 处理2的倍数
    while num % 2 == 0:
        factors.append(2)
        num //= 2
        if show_progress:
            current_time = time.perf_counter()
            # 只有当距离上次更新超过指定间隔，才更新进度
            if current_time - last_update_time >= update_interval:
                print(f"找到因子: 2, 剩余: {num}", end='\r')
                sys.stdout.flush()
                last_update_time = current_time
    
    # 处理奇数因子
    i = 3
    while i * i <= num:
        if show_progress:
            current_time = time.perf_counter()
            if current_time - last_update_time >= update_interval:
                # 显示当前正在尝试的因子和进度估计
                progress = min(100, int((original_num - num) / original_num * 100))
                print(f"尝试因子: {i:8d}, 剩余: {num:12d}, 估计进度: {progress}%", end='\r')
                sys.stdout.flush()
                last_update_time = current_time
            
        while num % i == 0:
            factors.append(i)
            num //= i
            if show_progress:
                current_time = time.perf_counter()
                if current_time - last_update_time >= update_interval:
                    progress = min(100, int((original_num - num) / original_num * 100))
                    print(f"找到因子: {i:8d}, 剩余: {num:12d}, 估计进度: {progress}%", end='\r')
                    sys.stdout.flush()
                    last_update_time = current_time
        i += 2
    
    # 如果剩下的数是一个质数
    if num > 1:
        factors.append(num)
        if show_progress:
            print(f"找到因子: {num:8d}, 剩余: 1, 估计进度: 100%", end='\r')
            sys.stdout.flush()
    
    if show_progress:
        print()  # 换行
    
    return factors

def main():
    try:
        user_input = input("请输入一个大于1的正整数: ")
        number = int(user_input)
        
        # 记录开始时间
        start_time = time.perf_counter()
        
        # 执行质因数分解并显示进度，设置0.1秒的更新间隔
        factors = prime_factors(number, show_progress=True, update_interval=0.1)
        
        # 记录结束时间并计算耗时
        end_time = time.perf_counter()
        elapsed_time = end_time - start_time
        
        # 格式化输出结果
        result = " × ".join(map(str, factors))
        print(f"\n{number} = {result}")
        print(f"分解耗时: {elapsed_time:.6f} 秒")
    
    except ValueError as e:
        print(f"输入错误: {e}")
    except Exception as e:
        print(f"发生错误: {e}")

if __name__ == "__main__":
    main()
    
``

这个假设在有了量子计算机后将不再成立，借助[秀尔算法](https://zh.wikipedia.org/wiki/%E7%A7%80%E7%88%BE%E6%BC%94%E7%AE%97%E6%B3%95)量子计算机可以以多项式时间解决因数分解问题。

- [为什么超级计算机60万年才能破解RSA密码，量子计算机只需3小时？ ](https://www.sohu.com/a/253519077_270867)
- [币圈巨震，量子霸权论盛行，比特币真能被破解吗？](https://xueqiu.com/6666553303/133429514)

> 传统算法（如试除法、Pollard's Rho 算法）的时间复杂度通常以 “整数本身的大小n” 为输入规模，例如试除法是$(O(\sqrt{n})$。
> 但在计算机科学中，输入规模的标准定义是 “输入数据的位数”（即二进制或十进制位数）。对于一个大整数n，其位数 $k \approx \log_2 n$（二进制）或 $k \approx \log_{10} n$（十进制），即 $n \approx 2^k$。
> 秀尔算法将大整数分解问题从 “指数时间（相对于输入位数）” 降为 “多项式时间（相对于输入位数）”

## 二、密码安全

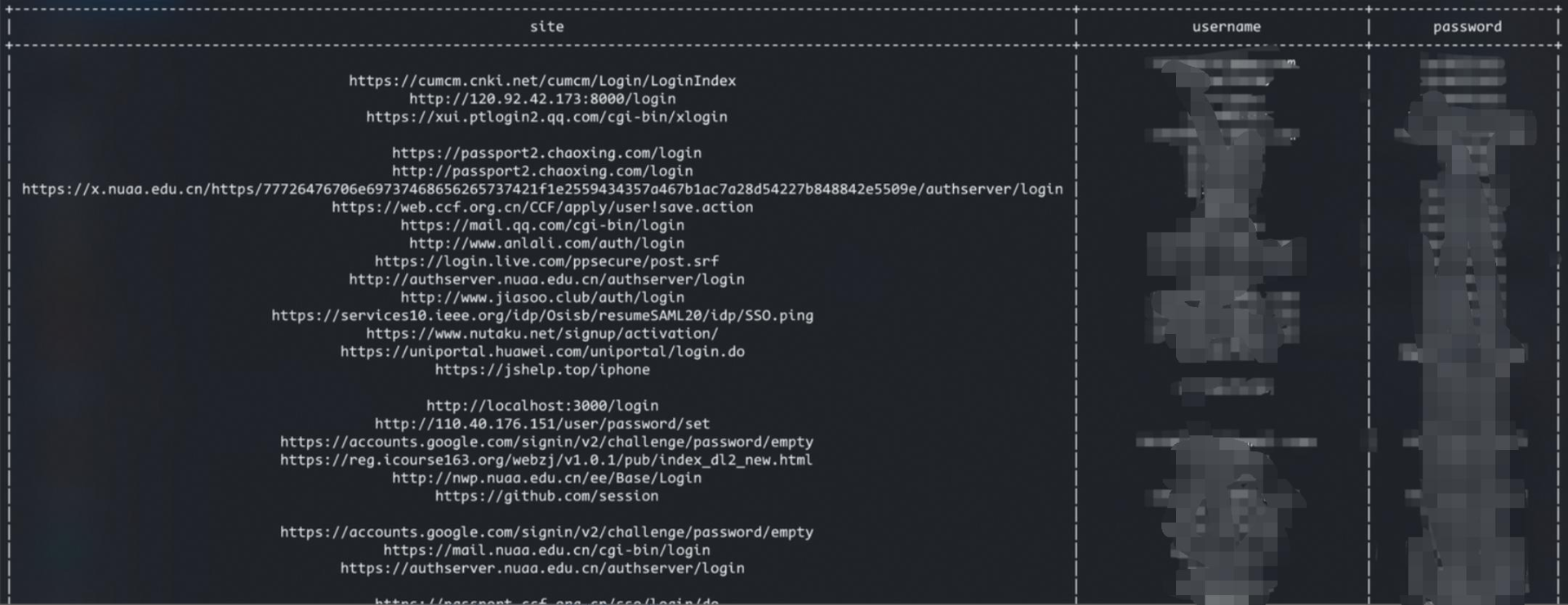
当然，现在就考虑量子计算机的威胁可能有点杞人忧天，但日常生活中我们的密码安全处境还是很糟糕。2019年，一个叫“[微博五亿手机号绑定数据](https://m.mp.oeeee.com/a/BAAFRD000020200324289835.html)”的文件在网络上流传，虽然官方并不承认被脱裤（即[拖库](https://wiki.mbalib.com/wiki/%E6%8B%96%E5%BA%93)，黑客盗走用户资料数据库）

我在这份数据中找到了自己的手机号和微博uid，随后注销了新浪微博，至今没有再次注册。

有个[在线网站](https://haveibeenpwned.com/)可以检查你的密码是否被泄露过（是否出现在已知泄露中）。检查泄露的机制使用了[基于散列的k-匿名化](https://zh.wikipedia.org/zh-cn/K-%E5%8C%BF%E5%90%8D%E6%80%A7#%E5%9F%BA%E4%BA%8E%E6%95%A3%E5%88%97%E7%9A%84k-%E5%8C%BF%E5%90%8D%E5%8C%96)机制，不会发送你的密码原文。

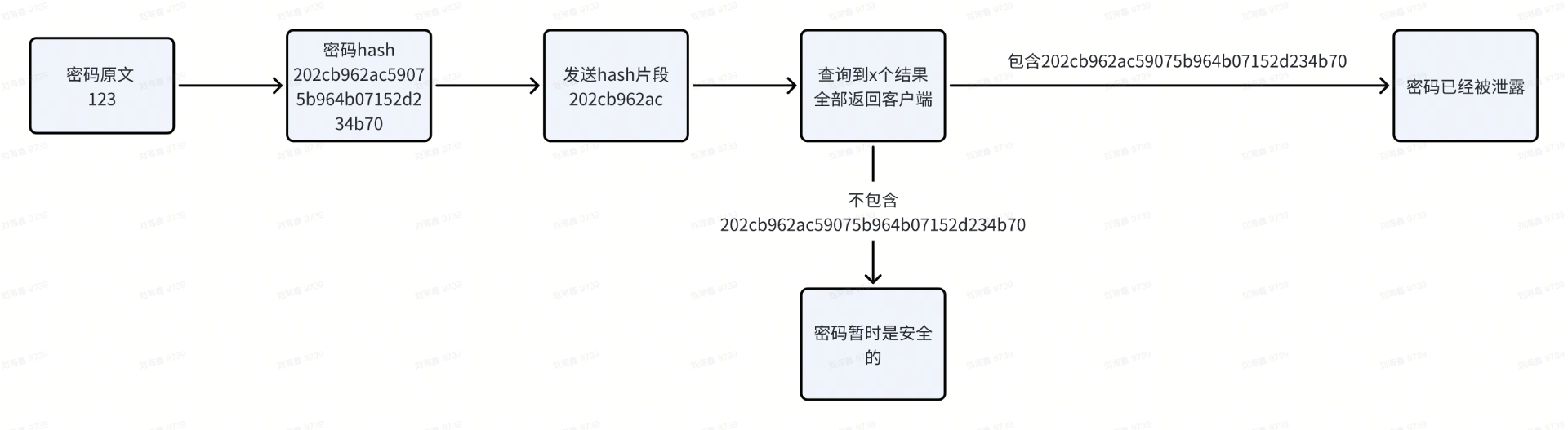
![验证密码是否泄漏过程](https://image2.ntutn.top/2025/07/e51b4c4fdf7010299ed896f4628478c3.png)

那么，如何安全地管理自己的密码呢？

### 复杂有意义的密码

初中的排列组合知识我们就知道，纯字母或数字密码强度很低，而网站一般不允许拿汉字当密码否则我们早无敌了。学会起一个安全而好记的密码就是一门学问了。

![密码强度](https://image2.ntutn.top/2025/07/c4fc66b2bc429c89fa9e4475d5262ef8.png)

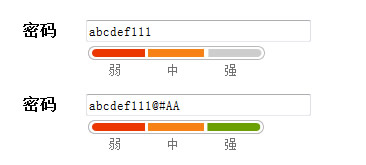
我的建议是，使用有意义的单词，但是用数字和特殊符号把完整的单词拆分开，这样不但用上了特殊符号，还保证了你密码任何一部分不出现在字典里，而且还好记。比如：

```plain
Dan/makuEng2ine

启用两步登陆

简单来说，两步登陆既要求你输入密码，又要求你使用手机验证码或其他方式验证。即使黑客通过撞库或者中间人攻击等方式拿到了你的密码，他也不大可能能同时拦截到你的短信验证码。

密码管理器

网上冲浪久了，我们肯定会注册一大堆网站，把这些密码全都记住显然不太可能，除非你把密码设置成一样的——那更不安全。选择一个密码管理器是值得考虑的事情。

这里提示的是，尽量不要用Google浏览器自带的密码管理功能，因为它保存的密码对你电脑上的其他程序是完全可见的，相当逆天。

Chrome保存密码并不安全

推荐的选择

这里我推荐Bitwarden，它跨平台，跨浏览器同步，且完全开源。对于一般使用来说Bitwarden的免费功能已经能满足要求，如果想用OTP验证密钥计算等高级功能才需要开会员。当然还可以私有部署，完全把数据掌握在自己手里。

Bitwarden

当然，就像使用钥匙圈也可能一次弄丢所有钥匙，遗忘Bitwarden类的密码管理器的主密码也会丢失所有的密码。

最后修改于 2025-07-24